Crystalline state | Law of symmetry – Plane of symmetry | Bragg’s Method of Crystal Analysis | Bragg’s X-ray spectrometer

Law of Crystallography-Crystalline state

Crystalline state – “The shape and size of crystals of a certain compound or element may vary with the conditions under which crystallization occurs, but the angles between the corresponding faces are always constant”.

 The term faces are referred to the surfaces which are usually, planar that bind the crystal.  The angle between the two interesting faces is known as the interfacial angle.

            For example- NaCl crystallizes in cubic found from an aqueous solution containing some area and faces shape if some amount of gum Arabic is present.

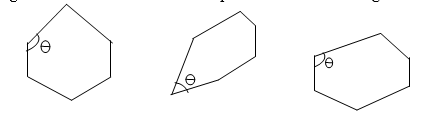
Fig 1:- Interfacial angles in crystals

Law of Symmetry

a. Plane of Symmetry

b. Axis of symmetry

c. Centre of symmetry

Plane of Symmetry

The plane of Symmetry is an imaginary plane passing through the crystal and dividing into two parts such that one part is the exact mirror image of the other part.

Fig2: Rectangular Planes in a cube

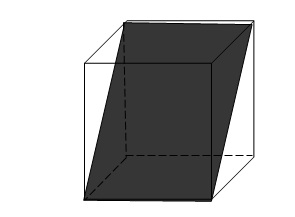
Fig 3: Diagonal Plane in a cube.

Axis of Symmetry

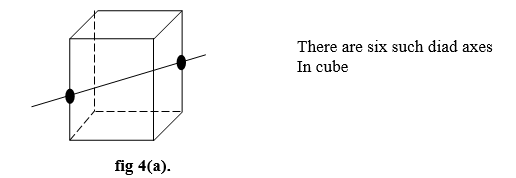
The Axis of Symmetry is an imaginary line about which the crystal is rotated so that the crystal presents the same appearance more than once in the course of a complete resolution through 360⁰.

• If the same appearance repeats after rotating through 180⁰, the axis is called a two-fold axis (and)
• In a cubic crystal, a diad axis passes through the midpoints of opposite edges as shown in fig 4(a).

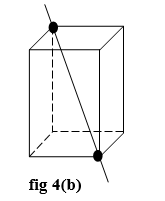
• If the same appearance repeats after rotating through 120⁰, the axis is called a three-fold axis (triad)

• There are four- triad axis in a cube.

• The tried axis passes through the opposite corners of the cube as shown in fig 4(b)

• If the same appearance repeats after rotating through 90⁰ give the same appearance, the axis is called a four-fold axis (tetrad)
• A cube has 3 tetrad axis which is right angles to each other.
• Fig 4(C) shows a tetrad axis that passes through the centres of pair of opposite faces of the cube.

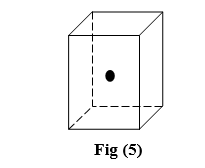
Centre of Symmetry                 

The Centre of symmetry is an imaginary point in the crystal such that any line drawn through it will intersect the surface of the crystal at equal distances in both directions.

Law of the rationality of indices

It is possible to choose along the three coordinate axes, unit distances (a, b, c) which may or may not be of equal length, such that the ratio of the three intercepts of any plane in the crystal is given by

Ma: nb: pc, where m, n and p are integral numbers.

If the intercepts are 2a, 3b and 3c the Weiss indices are 2, 3, 3.

“The Miller indices are obtained by taking the reciprocals at the Weiss indices multiplying them by the least common multiple (L.C.M.) of the Weiss indices and finally expressing the Miller indices in the forms of a simple ratio h:k:l. Where hkl are called the Miller indices of the plane.

100 Plane:-

The plane ABCD makes an intercept at ‘a’ on the x-axis but is parallel to the y and z-axes.

The ratio of the intercepts of the plane is a : ∞ : ∞.

The Weiss indices are 1: ∞: ∞ and the Miller indices are 1 : 1/∞: 1/∞ i.e. 1:0:0 the plane is designated as (100) plane.

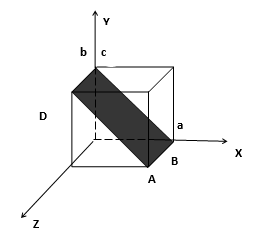
110 Plane:-

The plane ABCD makes intercepts ‘a’ and ‘b’ on the x and y axes respectively but is parallel to the z-axis.

The ratio of the intercepts is a:b: ∞.

The Weiss indices are 1:1: ∞ and the Miller indices are 1:1:1/ ∞  i.e. 1:1:0.                        

The plane is designated as (110) plane.

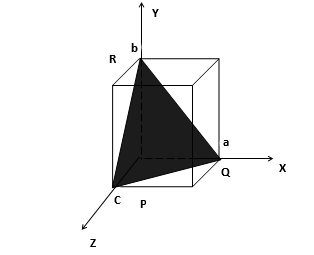
111 Plane

The Plane PQR makes intercepts a, b, c on x, y and z axes respectively.  The Weiss indices of the plane are 1:1:1 and the Miller indices are also 1:1:1.  The plane is designated as (111) plane.

Characteristics of Cubic Systems

Coordination number: – The number of equidistant nearest neighbours that an atom has in the given structure.

Primitive or simple cube.

In a simple cube, there is one atom at each corner.  This atom at the corner of the cube is shared equally by eight cubes meeting at the corner.  Hence, only 1/8^th of the mass of the atom belongs to the unit cell.  Since there are eight atoms at the eight corners of the cube, only ¹_/8 x 8 = 1 atom belongs to the unit cell.

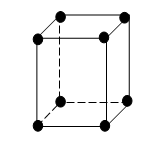
Coordination No. of a simple cubic lattice is six.  Eg. Only polonium at a certain temperature exhibits these structures.

Face-centred cube (F.C.C.)

In a face-centred cube or FCC, there is one atom at the centre of each of the six faces of the cube in addition to the eight atoms at the eight corners of the cube.  Each atom in the centre of the face is shared equally by two cubes.  Hence, one-half of the mass of the atom belongs to the unit cell.

                          ∴ ½ x 6 = 3 atoms belong to the unit cell.

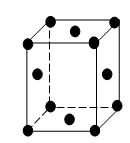
The coordination number of the F.C.C. lattice is 12.  Eg: Element Cu, Al, Pb and Ag exhibit this structure.

Body-centred cube (B.C.C.)

In a body-centred cube or BCC, there is one atom in the centre of the crystal in addition to eight atoms at the eight corners of the cube.  The atom in the centre belongs to the unit cell, and one atom amongst the corner atoms belongs to the unit cell.

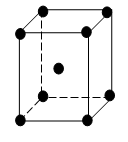
∴ 1+ 1 = 2 atoms belong to the unit cell.

 The coordination number of this structure is 8.

For eg: Element Li, Na, K and Cr exhibit this structure.

X-RAY diffraction method to study the crystal structure

Productions of X-rays: –

X-rays are produced in a Coolidge tube. It contains a tungsten cathode (c) which is concave in shape and emits electrons when heated electrically. These electrons impinge on an anticathode (T), whose front face is inclined to an angle of 45⁰ to the axis of cathode rays and give rise to x-rays.

The anti-cathode should have the following properties.

1) High melting point to withstand the high temperature developed due to the conversion of the energy of the impinging electrons into heat.

High thermal conductivity to dissipate the heat produced.

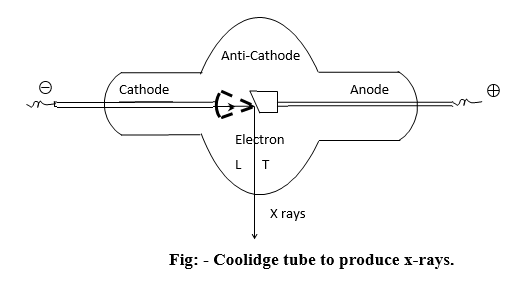
Hence, heavy hard metals like platinum, tantglum and tungsten are used as anticathode materials.  The tube is evacuated to a pressure of 10^-3 mm of Hg. A high potential difference of the order of 40,000 V is applied between the cathode and anode.

Properties of X rays

1) X-rays are electromagnetic radiations of wavelength between 10^-10 m to 10^-11m.

2) The penetrating power of X-rays is very high.

3) X-rays do not possess any charge, & hence they are not deflected either by an electric field or by a magnetic field.

4) X-rays of higher wavelengths are called ‘Soft rays’.  Whereas X-rays of cower wavelengths are called ‘hard rays’.

5) X-rays ionises gases, and also affect photographic plate.

6) X-rays produce fluorescence and phosphorescence in ZuS and/or barium Platino-cyanide coated screen.  

Bragg’s Method of Crystal Analysis

The condition for a reflection to give constructive interference depends on the interplanar distance d, angle of incidence θ of x-rays, the equation that relates these variables is known as Bragg’s equation.

Consider the parallel equidistant planes of atoms ions or molecules with interplanar distance d as shown in the diagram.

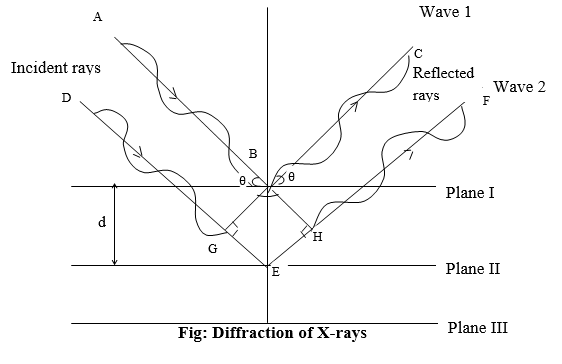
A parallel beam of monochromatic x-rays (AB and DG) of wavelength ⋋ strikes these planes at ∠θ.  The wave AB and DG are in the phase before striking planes, after striking successive planes the waves are considered to be reflected with an ∠θ of reflection which is equal to that of incidence ∠θ.  As explained above for constructive interference it is necessary that the waves reflected from successive planes should be in phase.

Considering the waves from planes (I) and (II), the initial parts of the two waves AB and DG were in the phase before reflection.  The wave reflected from the plane (II) travelled a greater distance than that from plane (I).  However, the parts of the reflected rays BC and HF must be in phase to give constructive interference.  This means that the extra distance that wave (2) travelled must be equal to either a whole wavelength or some integral number n of the ⋋ incident x-rays.

The extra distance the wave (2) travelled can be obtained by dropping from B the perpendicular BH and BG onto wave (2).  These perpendiculars make AB=DG and BC=HF.  The additional distance the wave (2) travelled is then simply GE+EH.  This must be equal to some integral multiple of ⋋ constructive interference.                        

Mathematically, for constructive interference, we can write the path difference,

GE + EH = n ⋋

                                          Where, n = 1, 2, 3….

                                          GBE  ∠θ

                                          ∴ sin θ =  GE / BE

                                          ∴ GE = BE sin θ

                                          GE = d sin θ     (As, BE = d)

                                          GE = EH = d sin θ

According to the above diagram the path difference

                          DEF – ABC = (DG+GE+EH+HF) – (AB+BC)       

                          Since, DG = AB

                                      HF = BC

                          ∴ Path difference = GE + EH = n ⋋

                          ie.  d sin θ + d sin θ = n⋋

                                          2dsin θ = n⋋

This is known as Bragg’s equation

Where n is an integer called the order of reflection. 

Bragg’s X-ray Spectrometer

The reflection angles and the intensities of the reflected beams corresponding to these angles can be determined with the help of Bragg’s X-ray spectrometer.

• The x-rays are generated in tube A by bombarding cathode rays on a suitable target B. The most commonly used metal targets are copper, molybdenum, and chromium.

• The generated X-rays are passed through a series of slits and filters (C,D etc.) in order to get a sharp monochromatic beam.  It is then directed to strike the face of a crystal E placed on a graduated rotating table F.  It may be rotated to any desired angle of incidence

• The reflected beam is passed into an ionization chamber G containing SO₂. The reflected X-rays ionize the SO₂ gas in proportion to their intensity.

• The extent of ionization and hence the intensity of reflection can be determined with the help of an electrometer.

• The experiment is repeated at various incident angles of X-rays and the angle at which maximum reflection occurs is determined.

• The current recorded in the electrometer is a direct measure of ionization produced which in turn is proportional to the intensity of the diffracted X-ray beams entering the ionization chamber.

• When the ionization current is plotted against the reflection angle θ we get an X-ray spectrum.

• The intensity of the diffracted X-ray beam decreases with the order of the spectrum.

Determination of interplanar distances using Bragg’s equation

From Bragg’s equation, we have n⋋ = 2dsinθ.  The X-rays are diffracted at the lattice planes and the reflection angle θ is measured using an X-ray spectrometer.                                   

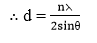
i.e. d ∝ 1/ sin 0, if X-rays of fixed wavelength are used for a given order of the spectrum, n.

Structure of NaCl and KCl

• Since NaCl and KCl are isomorphous compounds both of them should have a face-centered cubic structure but, because of X-ray scattering power differences, KCl shows a simple cubic structure.

• The X-ray scattering power of an atom or ion depends on the number of electrons associated with it.

• In KCl, the K⁺ and Cl^– have equal no. of electrons (18) and hence they scatter X-ray to the same extent.  As they have the same scattering power the unit cell of KCl shows a simple cubic structure.

• In NaCl, the Na⁺ ion has 10 electrons, whereas Cl^– ion has 18 electrons.  This results in a difference in their X-ray scattering powers.

• The (100) and (110) planes in both KCl and NaCl contain the same no. of K⁺ (or Na⁺) and Cl^‑ ion, hence, they show similar X-ray reflection.

But, the (111) planes in both KCl and NaCl are made up of alternate layers of K⁺ (or Na⁺) and Cl^– ions.

• The intensity of X-rays reflected by (111) planes containing Cl^– ions is very high compared to the intensity of Na+ ions.  Thus there is a difference in the intensity of X-rays reflected by Cl^– planes and Na⁺ planes.

• In the case, of KCl the intensities of X-ray reflected by K+ and Cl- planes are equal. Hence, these two reflected beams balance each other and no net reflection is obtained from (111) planes.  As a result, KCl unit cell behaves like a simple cubic structure.  But in NaCl, there is a net reflection from (111) panes.  Thus, the NaCl unit cell is a face-centered cubic structure.

Determination of Avogadro’s number

Avogadro’s number (N_A) is the number of molecules in one gram-mol of a compound.  Its value is 6.023 x 10²³ molecules mole.

The unit cell of NaCl consists of eight simple cubes which amount to 14 Na⁺ ions and 13 Cl^– ions.

i) There are 8 Na⁺ ions at the 8 corners of the unit cell and one Na⁺ ion at the centre of each of the 6 faces.

Each of the corner Na⁺ ions is equally shared by the eight-unit cells meeting at the corner.  Hence, 1/8^th of the mass of a corner Na⁺ ion belongs to one unit cell.

                    i.e. ¹/₈ x 8 = 1 Na⁺ ion belongs to the unit cell.

ii) The Na⁺ ion at the centre of each 6 faces is equally shared by the other two adjoining unit cells.

        Hence, ½ of the mass of the Na⁺ ion belongs to the unit cell.

                    i.e. ½ x 6 = 3 Na⁺ ion belongs to the unit cell.

        Thus, a total of 1+3 = 4Na⁺ ion belong to the unit cell.

Similarly, there are 12Cl^– ions at the middle of each of the 12 edges of the unit cell and one Cl^– ion is in the centre of the unit cell.  Each Cl^– ion at the middle of the edge of the unit cell is shared equally by four unit cells meeting along the edge.

                    i.e. ¼ x 12 = 3 Cl^– ions belong to the unit cell.

                    The Cl^– ion in the centre of the unit cell belong exclusively to the unit cell.

                    Thus, a total of 3+1 = 4Cl^– ions belong to the unit cell.

                    ∴ A unit cell of NaCl contains 4 molecules of NaCl.

Calculation of Volume of Unit cell

The mass of N_A (Avogadro’s number) of molecules of NaCl is M (mol wt)

Informative article

Crystal Field Theory | CFT | Crystal Field Splitting in Octahedral complexes | Crystal Field Splitting in Tetrahedral complexes.

FAQs