PHASE RULE | Gibb’s PHASE RULE, Example & applications

Introduction to Phase Rule

The phase rule is an important generalization dealing with the behavior of the heterogeneous system.

It is possible to predict qualitatively by means of a diagram the effect of changing pressure, temperature, and concentration at equilibrium.

Willard Gibb’s Phase Rule

Willard Gibb’s phase rule may be stated mathematically as F = C – P+2. Where F is the number of degrees of freedom, C is the number of components and P is the number of phases of the system.

Some Basic terms used in Phase Rule

Phase

A phase is defined as homogeneous, physically distinct, and mechanically separable parts of a heterogeneous system.

The phase should have a definite bounding surface.

Each phase can be separated from every other face by filtration, decantation, handpicking of crystals by shape and color, separation of one immiscible liquid from another using a separating funnel.

Number of phases (P)

It is the number of physically distinct states viz. solid, liquid, and gaseous present in the system at equilibrium.

A mixture of two or more gases or vapour is considered a single phase because there is no bounding surface between the different gases or vapours.

A mixture of two or more complete miscible liquids is considered a single phase as there is no surface of separation between them. Thus, alcohol and water will form one single phase.

A mixture of two immiscible liquids such as water and carbon tetrachloride will form two-phase and in addition, there will be a vapour phase.  Under certain conditions of temperature and pressure thus there will be three-phase.

Number of components (C)

It is the minimum number of independently variable constituents by means of which the composition of each phase.

Zero and negative values of components are permitted consider the following Examples

a) The water system consists of 3 phases i.e. ice, water, and vapour, in equilibrium.  The system can be represented as

           ice    ⇌    water   ⇌ vapour   or  H₂O_(s)  ⇌ H₂O₍₁₎  ⇌ H₂O_(g)     

           Each phase can be represented by one component system H₂O.

b)  Decomposition of calcium carbonate:

           When calcium carbonate is heated in a closed vessel the following equilibrium system results.

            CaCO₃            ⇌           CaO      +      CO₂             

            (Solid)                          (Solid)            (gas)

The Number of phases is three but the number of components is only two.

Degree of Freedom (F)

It is defined as the minimum number of variable factors such as pressure, temperature, and concentration which must be specified in order to define the system completely at equilibrium

a) Consider a one-component system existing in one single phase such as a system consisting of pure gas like Nitrogen.

           The two variables required to be specific, are temperature and pressure.

           Hence it is a bivariant system (F=2)

b) Consider a one-component system having 2 phases that are in the equilibrium of type,

Water   ⇌  Vapour

This system will have only one degree of freedom because at a given temperature it has only a fixed value of pressure.

Hence it is a univariant system (F=1)

c) Consider a one-component system having 3 phases which are in the equilibrium of type

ice   ⇌  water  ⇌ Vapour

The system can exist only at a definite temperature and pressure.

Hence such a system is called a non-variant or invariant system (F=0)

One component system

Application of Phase Rule to one component system

The Water  System

• Water exists in 3 states ie. Solid, liquid, and water vapour.
• As each phase is represented by one chemical constituent H2O, it is one component system.
• The phase diagram for the water system showing the effect of pressure and temperature on various equilibria is shown

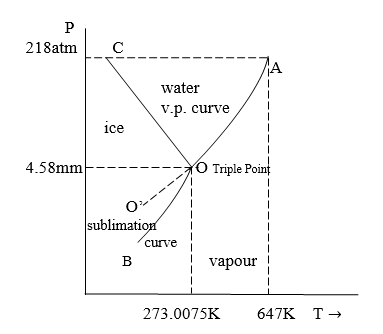
Description of the Phase diagram

Area:-  The area BOC, COA, and AOB represent solid, ice, liquid water, and water vapour respectively. Thus, within the areas water exists only in one phase.

           This curve is inclined away from both the axes indicating that the boiling point of water increases with an increase in pressure.

Curves:- Curve OA is the vapour pressure curve of water which represents equilibrium between liquid water and vapor. 

           The critical pressure and temperature of the water are 218 atm and 64K at point A.

ii) Curve OB is the sublimation curve of ice, which represents equilibrium between ice and water.

iii) Curve OC is a fusion curve, that represents the equilibrium between ice and liquid.  This curve is inclined toward the pressure axis indicating that as pressure increases the melting point of ice increases.

iv) Metastable state:-  The vapour pressure of the curve of water AC can be continued past the triple point as shown by the dashed line OO’. That is, water can be super-cooled by carefully eliminating Solid particles. The super-cooled water system ice/vapor on the slightest disturbance or introduction a crystal of ice.

C) Triple Point:-  The 3 curves OA, OB, and OC meet at point O, called the triple point.

           At this point, the three phases, ice, water, and vapour are in equilibrium.

Application of Phase Rule to water system

a) For Areas:-

           Within the areas, BOC [ice], COA [liquid], and AOB [vapour] water exist only in one phase.

           The degree of freedom F = C-P+2  =    1-1+2=2

           Thus, within areas it is bivariant can be completely defined by two variables ie. Temperature and pressure.

b) Along Curves:-

           Along curves, OA (water  ⇌ vapour) OB (ice ⇌ vapour), and OC (ice ⇌ water) the two phases are in equilibrium, and the degree of freedom is one.

           Thus along the curve system is a mono variant, completely defined by one variable either pressure or temperature.  

c) At triple point:-

           At point O all three phases are in equilibrium with the degree of freedom of Zero. (F=0). Thus point O is non-variant and exists only at a very low pressure of 4.58 mm and a low temperature of 273.0075K.

The Sulphur System

Sulphur can exist in four phases as

i)   Rhombic Sulphur (S_R) ………….Solid-phase

ii)  Monoclinic Sulphur (S_M) ………Solid-phase

iii) Sulphur vapour (S_V) …………….Vapour Phase

iv) Sulphur liquid (S_L) ……………..Liquid phase.         

It is also one component system since sulphur is the only individual chemical representing the various phase.

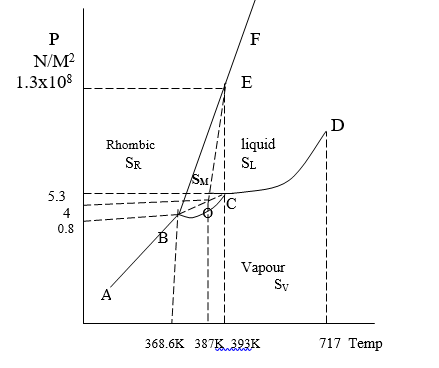
1) Areas: In sulphur system, there are four areas:

i)  Area below ABCD: It contains only sulphur vapour (S_V)

ii) Area ABEF: It contains only Rhombic (S_R)

iii) Area BEC: It contains only monoclinic Sulphur (S_M)

iv) Area DCEF: It contains only liquid sulphur (S_L)     

2) Curves:-

            The curve is the sublimation curve of Rhombic sulphur where rhombic Sulphur (SR) and Vapour Suphur (SV) is in equilibrium at point 368.6K.

            The curve BC is the sublimation curve of monoclinic suphur where monoclinic sulphur and vapour sulphur (SV) is in equilibrium at point 393K.

            The curve CD is vapour pressure curve of liquid sulphur, here liquid sulphur (S_L) and vapour liquid (S_V) is in equilibrium at point 717K.

            The Curve BE is the transition curve of Rhombic Sulphur here rhombic sulphur and monoclinic sulphur or in equilibrium.

            This curve is inclined away from the pressure axis indicating that as pressure increases the transition temperature of the Rhombic Sulphur also increases.

            The Curve CE is a fusion curve of monoclinic sulphur, here monoclinic sulphur and liquid sulphur are in equilibrium.

            The Curve EF is the fusion curve of Rhombic Sulphur, here Rhombic sulphur and liquid sulphur are in equilibrium.

            Curve CE and EF have inclined away from both the axes indicating that increases in pressure increase the melting point of rhombic sulphur as well as monoclinic sulphur.

Metastable Equlibrium

1. The dotted line BO is the sublimation curve of metastable rhombic sulphur.

Heating Must be gradual for transition to take place but if heating is rapid, the transition cannot take place, curve of rhombic sulphur extends beyond point B till temperature 387K.

ii) The dotted line CO is vapour pressure curve of metastable liquid sulphur.

If liquid sulphur cooled rapidly along with DC then solid monoclinic sulphur may not appear at point C.

iii) The dotted line EO is the fusion curve of the rhombic sulphur curve is inclined away from both the axes indicating that increases in pressure increase the melting point of metastable rhombic sulphur.

Triple Point

i) The three phases are in equilibrium at point B

            S_R −  S_M − S_V

ii) At triple point C

            S_M −  S_L − S_V

iii) At triple point E

            S_M −  S_R – S_L

iv) At Metastable triple point O

            S_R −  S_L − S_V

Application of Phase Rule to sulphur system

a) For areas:

          Within the areas, ABEF all from sulphur exists in one phase. The degree of freedom    F =2.

            Thus it is bivariant and it can be completely defined by two variables such as pressure and temperature.

b) Along curves:

            Along each of curves AB, BC, CD, BE, CE, and EF two phases of one component are in equilibrium. 

            The degree of freedom F = 1

            Thus it is a mono variant and can be completely defined by one variable either pressure or temperature.

c) Triple point:

            At 4 triple points B, E, O, C three phases of one component are in equilibrium.

            The degree of Freedom F = 0.

            The system is non-variant and it exists only on particular values of pressure and temperature.

Two-component system

Eutectic System and Phase diagram of two-component System

Lead Silver System

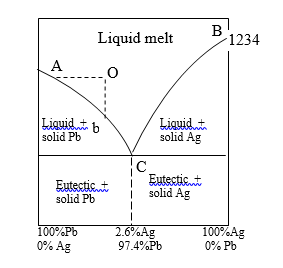
1) Curve AC:

            The freezing point of the curve of Pb: A represents the freezing point of the melting point of solid lead and the curve AC shows that the addition of silver lowers the melting point along with it.

            The phases that are in equilibrium along AC are solid lead and a solution of silver and lead.

            Applying the reduced phase rule equation

                        F = C-P+1   = 2-2+1 = 1

            Thus the system is monovariant.

2) Curve BC;

            The freezing point of curve Ag: B represents the melting point of solid silver and curve BC shows that the melting point is lowered by the addition of lead.

            The phase-in equilibrium along BC is solid silver and lead solution.

            The system is mono variant.

3) The Eutectic Point C:

            The curve AC and BC interest at C, which is called the Eutectic point.

            Here are three phases solid Ag, solid Pb, and solution of equilibrium.

            Applying the reduced phase rule equation.

                        F = C-P+2  = 2-3+1 =0

            Thus, the system at C is mono variant.  Both the variables, temperature (576K) and composition (97.4% Pb and 2.6% Ag) are fixed.

            If you raise the temperature above the eutectic temperature the solid phase Ag and Pb disappear and if it cooled below, will land in the solid Ag/Pb area where the solution phase is non-existent.

4) The area above AOC

            This region represents the single-phase system, the solution of molten Ag and Pb.

            Applying reduced phase rule equation

                        F = C-P+1  = 2-1+1 = 2

            Thus system along AOC is bivariant.

            The area below AC represents the phase Pb + solution, while that below BC the phases Ag + Solution.

            While below BC the phases Ag + Solution.

            The area below temperature 576K represents solid Pb + Solid Ag.  All these areas have two phases and one degree of Freedom 

             F = C-P+1 = 2-2+1 = 1.

Application OR  Desilverisation

1) The Pb – Ag system has special significance in the Desilverisation of molten argentiferous lead.

2) The argentiferous lead containing a small percentage of silver is first heated to a temperature above 600K.

3) It is then allowed to cool, and the temperature will fall along the line ab.

4) When point b is reached, the lead will crystallize out and the solution will be richer with respect to silver.

5) Cooling is continued, when lead continues to separate out, which is constantly removed by the process of cupellation.

Three-component system

The maximum degree of freedom is possible when P is minimum which is one in and system.

Thus according to the phase rule equation, the degree of freedom having P as one is four.

                        F = C-P+2    =   3-1+2=4

In order to simplify the graphical representation for three components, the procedure generally adopted is to consider the condensed system, that is the vapour pressure is neglected at a constant temperature, then according to condensed phase rule  F = C-P+1     =      3-1+1 =3

Representation of ternary system.

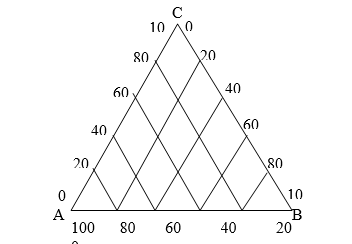
1) Each apex represents the pure component ie. A represents 100% of A, B represents 100% B, and C that 100% C.

2) Any point situated on any side of the triangle represents a binary system. For example point, P represents 40% C and 60% A

3) Any point located within the triangle represents a ternary system.  For example, point R represents 40% A, 20% C, and 40% B.

System composed of three liquids having partial miscible.

Type I: Formation of one pair of partially miscible liquids.

Type II: Formation of two pairs of partially miscible liquids.

Type III: Formation of three pairs of partially Miscible liquids.

One pair of partially miscible liquids:

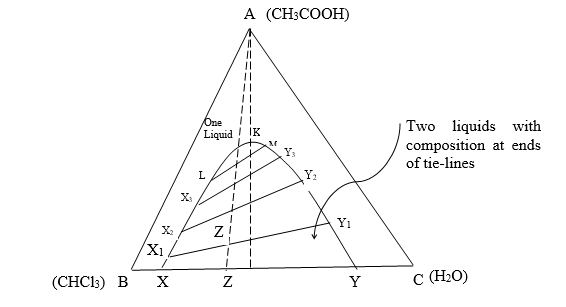
Consider 3 liquids A, B, and C

The liquids B and C are miscible in each other at a given temperature and pressure and the third liquid A is completely miscible in both the liquids B and C.

If two liquids are mixed thoroughly some C dissolve in B and some B dissolves in C and they form two conjugate solutions having their composition represented by points x and y online.  The line x, and y passing through Z₁ is called a tie-line.

If component A is relatively more soluble in the layer rich in C than it is in the layer rich in B, then obviously the state point of the layer rich in C will be nearer to the apex A than that of the layer rich in B.

As more as A is added the tie-line becomes shorter till these merge to a point K.

The limiting values of the misciblities of B in C and C in B in presence of A outside this curve XKY for any composition, the ternary system will be homogeneous and inside the system is heterogeneous.

The curve XKY is called the binodal curve.

The composition of two layers at this point becomes identical and point K is called the plait point.

This is an invariant point.

A point outside the binodal curve XKY represents one liquid layer only.

According to the phase rule, such a system can be completely defined if the values of two degrees of freedom apart from temperature and pressure are stated. These two degrees of freedom are the two composition terms corresponding to any of the two components of the liquid phase.

You can also read about Fluorescence-phosphorescence-spectroscopy

FAQs