Basics of Colloids | Classification of colloids | Electrokinetic  Phenomena – Electrophoresis and Electroosmosis

Classification of Colloids

Lyophobic Colloids (Solvent hating)

In this type, the affinity between the dispersed phase and the dispersion medium is very small. Hence these solutions are called solvent hating, these are relatively unstable compared with lyophilic solutions. They can be easily coagulated and it is difficult to get back to the coagulated dispersed phase in the colloidal state. Thus they are irreversible colloids.

e.g.: various metal solutions, Arsenic, and sulfide solution.

Lyophilic Colloids (Solvent loving)

In this type, there is a considerable affinity between the dispersed phase and dispersion medium.  Hence these solutions are called solvent-loving.  The coagulation is not as easy as that of a lyophobic solution.  Hence they are more stable & are reversible colloids.

eg: Jam, gelatin, starch, etc.

Origin of charge on colloidal particles:- Reason for the charge on colloidal particles

Self dissociations

The particles of soap, detergent, etc. possess a charge due to self-dissociation.  The soaps are Na⁺ or K⁺, Salt of long-chain fatty acids, they dissociated in solution giving ions.

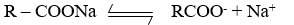
The anion (R – COO^–) has a strong affinity for each other, therefore, these ions aggregate colloidal particles.

Medium/P^H of the solution

The charge on colloidal particles is due to the medium in which they are present. e.g. Protein. 

They are positively charged in an acidic medium and negatively charged in a basic medium.

Amino acids are the building units of protein in an acidic medium, –the NH2 group accepts a proton from acid and becomes positively charged.

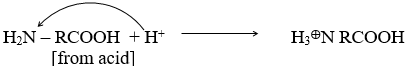
In the basic medium the –COOH group donates a proton and becomes negatively charged.

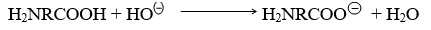
Preferential adsorption

The adsorption of certain kinds of ions from the dispersion medium on the colloidal particle is also one of the reasons for the existence of charge.  The type of charge depends on the way by which the solution is prepared. 

eg:- let us consider an example of AgI Solⁿ. In excess of KI, Solⁿ is added to a dilute solution of AgNO3, and the AgI solution adsorbs.  I^⊝ ions & forms a negative colloid and if excess of AgNO₃ solution is added to a dilute solution of  KI the AgI solution adsorbs Ag^⊕ ions & forms +Ve colloid.

Helmholtz Electrical Double Layer

The colloidal particle carries an electric charge +ve or –ve. Due to this charge, they repel one another and this solution becomes stable.  But the charged colloidal particles will attract.

Oppositely charged ions present in the medium. The electrical potential corresponding to such a charge distribution is also shown.

Such double layers are supposed to exist not only on plane surfaces but also surrounding solid particles suspended in a liquid medium.  The value of potential developed between the surface and fixed layer in solution is termed as zeta potential given by,

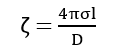
Helmholtz’s model of the double layer is found to be inadequate since the thermal motion of the liquid molecules could rarely permit such a rigid placement of charges at the interface.  Much more reasonable therefore it is diffused double layer proposed by the stern.

This model assumes that ions are held in an immobile manner even though they are present in Solution it does not take the mobility of particles in a liquid medium.  The fall of potential as moved away from the surface is linear and abrupt zeta potential is measured between the surface and 1st layer (fixed layer) it cannot be used to explain electrokinetic phenomena.

Stern’s Theory

Stern Theory shows that the electrical double layer consists of two parts:-

i) One part of the double layer is fixed to the solid surface and is known as the fixed part of the double layer.

ii) The second part extends some distance into the liquid phase and is known as diffused.

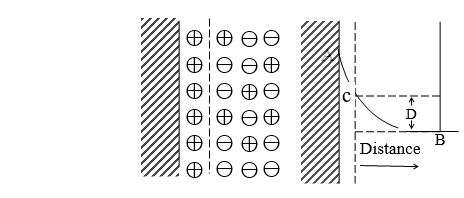
In this part, the movement of the particles is free due to thermal agitation.  The distribution of positive and negative charges is not uniform here so the whole potential difference between the colloidal particles and the dispersion medium consists of two parts.

i) Potential difference between the particle (colloidal) and the dispersion medium (solvent) layer (A)

ii) Potential  difference  between the dispersion  medium  (liquid)  layer and body of the medium (B)

Thus, the after-potential difference is known as electrokinetic potential or zeta potential. 

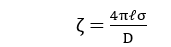
where ℓ = thickness of the double layer

                   σ = amount of charge per sq. cm.

                   D = dielectric const. of condenser

Thus be designed as the potential difference between the solution (Colloid) particles and dispersion (solvent ions) medium.

Electrokinetic  Phenomena

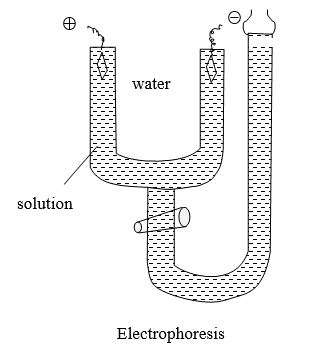
Electrophoresis

The unidirectional migration of colloidal particles under the influence of an electric field is called “electrophoresis” (cataphoresis). Colloidal particles Carry the same type of charge under particular conditions. Hence when they are kept under the influence of electric potential, they move to the oppositely charged electrode by electrostatic attraction. The electrostatic force of repulsion present prevents colloidal particles aggregate together.

The electrophoresis can be utilized to measure the rate with which the colloidal particles migrate it is normally expressed in the term of electrophoretic mobility (μ). It is defined as the distance traveled by a particle in one second under the potential gradient of one volt per cm.  Hence the process of electrophoresis can be used to separate the component of the mixture. Electrophoresis is used for the separation of proteins, nucleic acid, polysaccharides, etc.

where n= viscosity of the medium

           D = dielectric constant of the medium

The surface behavior can also be studied by changing the P^H, and ionic strength of the solution.  Zeta potential (ζ) & electrophoretic mobility (μ) are related by this equation.

Electro osmosis

The migration of dispersion medium under the influence of an applied electric field (in which electrophoresis is prevented) in presence of a semipermeable membrane is known as electroosmosis

If particles carry a negative charge the dispersion medium will have toward the negative electrode and if particles are positively charged, the dispersion medium will move toward the positive electrode.

When equilibrium is reached backward pressure is created due to the difference in height of the capillary column balance electroosmotic flow.  This pressure is known as electroosmotic pressure P.

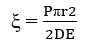
Where r = radius of the capillary

              E = applied potential

              D = dielectric constant of the medium

Colloidal Electrolyte [formation of Micelles]

Potassium Oleate is a typical example of a class of compounds known as colloidal electrolytes or association colloids.

If potassium Oleate is added to the small increasing amount of water at 323k, it dissolves in water and forms K⁺ and Oleate ions. 

The surface tension of the solution continuously decreases from that of pure water and the solution behaves like any other strong electrolyte in that the molar conductivity is a linear function of the square root of concentration. 

The colloidal aggregates formed in the solvent are referred to as micelles.

The concentration at which micelles appear is called the Critical Micellisation Concentration (CMC).

The change from ions into Micelles is reversible and the Micelles can be destroyed by diluting the solution.

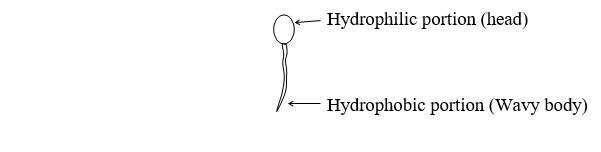
The accepted structure of  Micelles is an approximately spherical body, with hydrophilic groups on the surface and hydrophobic groups directed towards the interior.

          The wavy line represents the hydrophobic portion and the circle represents the hydrophilic portion.           Laminar Micelles have also been identified.

Sedimentation (DORN EFFECT)

Sedimentation potential is opposite to that of electrophoresis.  It is an electrokinetic phenomenon.  Colloidal Solutions are fairly stable, if they are kept for a long time under the influence of gravity the particles start moving downward.  It is a very slow process, the heavier particles get distributed downward and the lighter particles upward.  Such movement  & distribution of colloidal particles under the influence of gravity is known as sedimentation.  The potential difference developed between the lower layer and the upper layer is known as sedimentation potential.  The effect was observed by Dorn, hence it is known as Dorn Effect at different layers. Introducing suitable electrodes at different layers.

Streaming Potential

The potential developed when a colloidal solution is forced to pass through a porous membrane or capillary is known as streaming potential.

The streaming potential effect can be regarded as the reverse of electroosmosis.  In electroosmosis flow of liquid take place. Due to applied potential while the streaming potential is developed due to the flow of liquid.

The streaming potential is measured by keeping two calomel electrodes on the two sides of the Porous membrane.

Streaming Potentials (S) & Zeta Potential (ξ) are related by the equation,

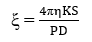
Where, η = Viscosity of Solⁿ,

             D = Dielectric constant of the solution

             K = Specific conductance of solution,             

 P = Driving pressure applied to streaming Solⁿ

Donnan membrane equilibrium

It is Donnan membrane equilibrium when large non-diffusible ions are separated by a diffusible salt from a diffusion membrane at equilibrium, it is expected that the diffusible ion should get distributed equally on both the sides of membrane consider a simple example in which an equal volume of the solution of the sodium salt of a protein (Nap) and of sodium chloride (NaCl) with respect to equivalent concentration C1 and C2 are initially separated by a semipermeable membrane. Here protein ions are non-diffusible and chloride ions are diffusible ions.

At equilibrium, let a certain amount x of sodium and chloride ions pass and the concentration is known from thermodynamics that at equilibrium. The chemical potential of sodium chloride present on both sides of the membrane must be the same  and the  chemical potential of  any substance in terms of its activity ‘a’ can be represented in terms of concentration for dilute solution (a = c)

                                    a = (NaCl)₁ = a (NaCl) ₂                              ….(1)

            but,            a(NaCl) = a (Na⁺) + a (Cl^–)              …..(2)

            ∴ equation (1) can be written as

                        a (Na⁺)₁ a(Cl^–)₁ = a(Na⁺)₂ a(Cl^–)₂                   …..(3)

For dilute solutions, the ionic activity may be replaced by the corresponding concentration.

            ∴ (C₁ + X) X = (C₂ – X)  (C₂ – X)                …..(4)

               C₁ X + X² =  C₂² – 2 C₂X + X²

               ∴ C₁X + 2 C₂X = C₂²

                 X (C₁ + 2C₂)    = C₂²

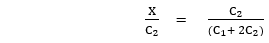
For this eqⁿ, the fraction of NaCl that has diffused through the membrane, when equilibrium is attained, depends on C₁, i.e. the Concⁿ of Nap is C₁ is large the fraction diffused would be small .when C₁ is small as compared to C₂ .

The equation is known as Donnan membrane equilibrium.

FAQs