Introduction – Surface Chemistry
Surface chemistry is the study of the phenomena that take place on the surfaces of substances like adsorption, colloids, etc.

Surface chemistry is the study of physical and chemical phenomena observed on the surface, including solid-liquid interfaces, solid-gas interfaces, solid–vacuum interfaces, and liquid-gas interfaces.
The variation of the amount of gas adsorbed by an adsorbent with equilibrium pressure at constant temperature is called “adsorption isotherm”.
Surface Chemistry Adsorption Isotherms
Freundlich Adsorption Isotherm
Freundlich proposed an empirical relation between the amount of gas adsorbed per unit mass of adsorbent ie. 𝒳/𝓂 and the equilibrium pressure ‘p’ at a constant temperature. Which is known as Freundlich’s adsorption isotherm represented as,

Where ‘𝓍’ is the mass of gas adsorbed by ‘𝓂’ gm of adsorbent. ‘P’ is the pressure of the gas in the space above the adsorbent and ‘k ’and ‘n’ are constant for the given system and temperature.
By taking the logarithm of equation (I) we get,
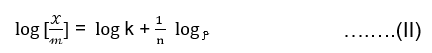
The plot of x/m against log p should give a straight line with an intercept on the y-axis equal to log k and slope = 1/n.

The actual plots show a slight curvature, especially at low temperatures. Thus, Freundlich adsorption isotherm is found to be approximate although it is still frequently used in connection with adsorption from solution.
Langmuir’s Adsorption Isotherm
In 1916 Langmuir suggested the theory of the adsorption of gases on solids. It is known as “Langmuir’s unimolecular adsorption isotherm”.
This isotherm is based on the following assumptions
a. In chemisorptions, a chemical bond is formed between the molecules of adsorbate and adsorbent. Since the intramolecular forces fall off rapidly with distance adsorbed layers are not likely to be more than one molecular layer in thickness.
b. The rate of adsorption is proportional to the unoccupied surface area of the adsorbent.
c. The rate of adsorption of molecules is also proportional to the pressure of the gas.
d. The adsorption process consists of two opposing processes,
i. The molecules get adsorbed on the surface (adsorption),
ii. The adsorbed molecules leave the surface (desorption)
e. When the rate of adsorption becomes equal to the rate of desorption, the process attains equilibrium, which is called adsorption equilibrium.
f. The gas under study behaves ideally.
Based on this assumption, Langmuir derived an equation
Consider the unit area of an adsorbing surface exposed to a gas. Molecules of the gas will strike the surface and get adsorbed, While other molecules will tend to desorb or evaporate from the surface.
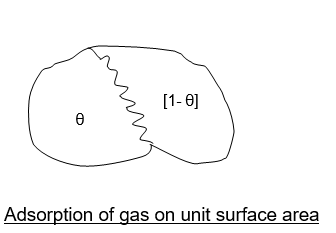
The fraction‘ θ’ of the adsorbing surface is covered by gas molecules.
The fraction (1- θ) will be bare.
∴ Adsorption can take place on the bare surface,
∴ Rate of adsorption = Kap (1- θ) ……(I)
Where p – is the pressure of the gas
Ka – is a proportionality constant
The rate at which desorption will take place will be directly proportional to the area ‘θ’ covered by gas molecules.
∴ Rate of desorption = kdθ …… (II)
Where kd is the proportionality constant.
At adsorption equilibrium, the rate of adsorption and rate of desorption will be equal,
kap (1- θ) = kdθ ……(III)
kdθ = kap – kapθ
kap = kdθ + kapθ
kap = [kd + kap] θ

Dividing through the numerator and denominator of the RHS of equation (IV) by kd gives,
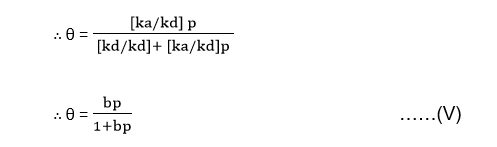
Where b = ka/kd is the adsorption coefficient
If ν is the volume of gas adsorbed per unit mass of adsorbent.
νm is the volume of gas required to completely cover the unit mass of adsorbent by a monolayer,

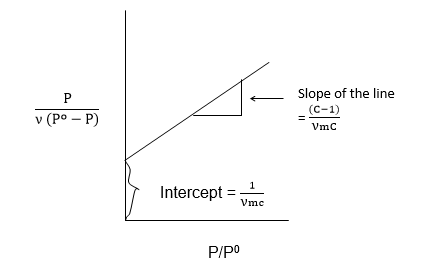
Graph plot of p/ν against p should give a straight line of slope 1/νm and an intercept of

Assumes different forms under different condition
Case I:- At very low pressure the term bp is very small
ν = νmbp
∴ ν ∝ p
Case II – At very high pressure, be is a very large
∴ ν = νm
Case III – At intermediate pressure Langmuir adsorption isotherm.
ν = kp1/n
n = integral value.
Types of Adsorption Isotherms
A large number of adsorption isotherms of many of the gases on a variety of adsorbents at different temperatures have been studied. Brunauer has classified these isotherms into five characteristic types which are shown below.
Two important phenomena are involved in physical adsorption.
Monolayer adsorption and multilayer adsorption
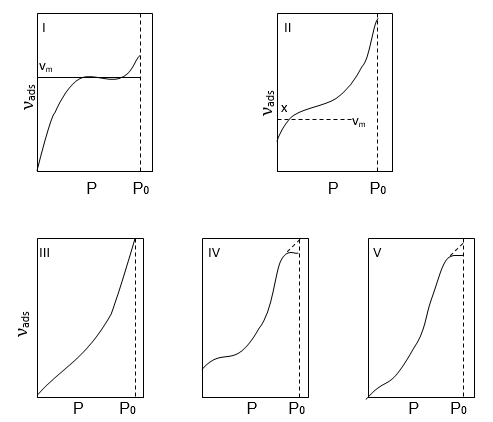
Brunauer’s classification of adsorption isotherms
Above figure ‘νads’ is the volume of gas adsorbed per unit mass of adsorbent at a pressure p and P0 is the saturated vapour pressure at the experimental temperature, i.e. the pressure required to condense the gas to liquid.
Type I
Isotherm shows a fairly rapid rise in the amount of adsorption with increasing pressure up to a limiting value νm i.e. the volume of gas required to cover the unit mass of adsorbent with a complete monolayer. This type of curve is obtained when adsorption is restricted to a monolayer. Adsorption of ammonia on Charcoal at 273k.
Type II
Isotherms represent multilayer physical adsorption on non-porous solids. Multilayer type of adsorption is possible when the gas pressure is increased, due to which the Vander Waal’s forces of the gas molecules in the first layer hold a second and so on. Point x in the figure represents the adsorbed volume necessary to form a monolayer of gas on the surface. Similar isotherms are obtained for physical adsorption on microporous solids but point x represents- both monolayer adsorptions on the surface as a whole and condensation in the fine pores. The remaining part of the curve represents multilayer adsorption for nonporous solids. Adsorption of nitrogen on Silica gel at 77k.
Type III and Type V
Show no rapid uptake of gas and occur when the forces at adsorption in the first monolayer are relatively small.
For Type III:- adsorption of bromine on Silica gel at 352 k.
For Type V:- Adsorption of water vapour on charcoal at 373k.
Type IV Has been observed in those cases in which there is a possibility of condensation of gases in the minute capillary pores of the adsorbent at pressure even below the saturation pressure Po of the gas. An example, Type IV is furnished by the adsorption of benzene on Fe2O3 at 323k.
The B.E.T. Equation for multimolecular Adsorption
The Langmuir isotherm ignores the possibility that the initial monolayer may act as a substrate for further physical adsorption. In B.E.T. isotherm, it deals with multilayer adsorption. This isotherm is due to Stephen Brunauer, Paul Emmett, and Edward Teller, hence the name B.E.T. isotherm.
Postulates of B.E.T. Equation
i. Langmuir adsorption theory with restricted to the formation of the monomolecular layer of the gas molecules on the solid surface and disregards the possibility that multilayer adsorption may also take place.
ii. B.E.T. theory assumes that physical adsorption resulting in the formation of a multilayer is the true picture of adsorption.
iii. In the B.E.T. Theory it is assumed that the solid surface possesses uniform localized sites and that adsorption at one site does not affect adsorption at the neighboring site as assumed in Langmuir theory.
iv. If it is further assumed that molecules can be adsorbed in the 2nd, 3rd…..nth layers. The surface area available for the nth layer is equal to the coverage of the (n-1)th layer.
v. The energy of adsorption in the 1st layer E1 is assumed to be constant and that in the successive layers is assumed to be E1 i.e. energy of liquefaction of gas.
Based on the above postulates B.E.T. derived the following equation known as the B.E.T. equation.

Where ν = equilibrium volume of gas adsorbed per unit mass of adsorbent at
pressure P and constant temperature T.
Po = Saturated vapour pressure at the same temperature.
νm= volume of the gas required to cover the unit mass of adsorbent with an unimolecular layer.
C = a constant for a given adsorbent.
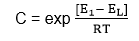
Where E1 – is the heat of adsorption in the 1st layer.
EL – is the heat of liquefaction of the gas.

Determination of Surface Area of Adsorbents
Surface area possessed by finely divided solids is of great significance not only in adsorption but also in catalysis. The B.E.T. method is based on the assumption that in the adsorption of gases.
From the B.E.T. equation
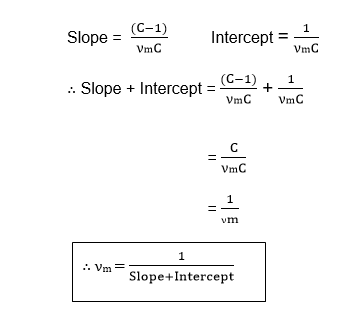
Therefore, the value of νm is the volume of the gas required to cover the unit mass of the adsorbent with an unimolecular layer can be obtained from the values of slope and Intercept.
This volume is reduced to N.T.P. (S.T.P.) conditions. Let, Po and To be the standard condition of temperature and pressure, and n be the no. of moles of the gas adsorbed.
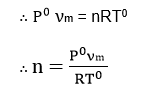
If, NA is Avogadro number then, the number of molecules of gas adsorbed = n x NA.
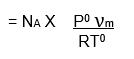
If σ is the area occupied by each molecule then the surface area of the given adsorbent is,
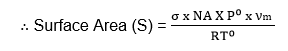
Nitrogen is commonly used as the adsorbate in the determination of the surface area of a given adsorbent. The region is it has a high value of C which gives well-defined, points in the adsorption isotherm.
Useful Articles –
Basics of Colloids | Classification of Colloids | Electrokinetic Phenomena – Electrophoresis and Electroosmosis
The following are the properties of Colloidal
1. Colloidal particles scatter the light.
2. Colloids are heterogeneous mixtures. Read more
MOLECULAR SPECTROSCOPY AND SOME BASIC CONCEPTS
Spectroscopy is the study of the interaction between matter and radiation. When the light has been absorbed by the molecule there is some change in the behaviors of the molecule observed. Read more…
FAQs
What is surface chemistry?
It is the study of the phenomena that take place on the surfaces of substances like adsorption.
Which is the Freundlich adsorption isotherm equation?
In the equation – x/m = k.P1/n (n > 1), Where ‘𝓍’ is the mass of gas adsorbed by ‘𝓂’ gm of adsorbent. ‘P’ is the pressure of the gas in the space above the adsorbent and ‘k ’and ‘n’ are constant for the given system and temperature.
What is BET method used for?
BET equation is used to determine the specific surface area of porous materials, including amorphous and crystalline materials.